Quick summary ↬ In this article we apply dynamic programming to one of the hard leetcode problem: 1335. Minimum Difficulty of a Job Schedule and explore ideas and different solutions.
Problem statement
You want to schedule a list of jobs in d days. Jobs are dependent and sequential in nature. Example: to complete the job i+1, you need to complete the job i and anything before that.
The core condition is every day you need to complete atleast one job. The difficulty of Job Schedule is sum of difficulty of each day of the d days. The difficulty of a day is maximum difficulty of the job done on that day.
Input: An integer array which represents the Job Difficulty and an integer d. The difficulty of ith job is represented by JobDifficulty[i].
Return maximum difficulty of job schedule. If you cannot find just return -1
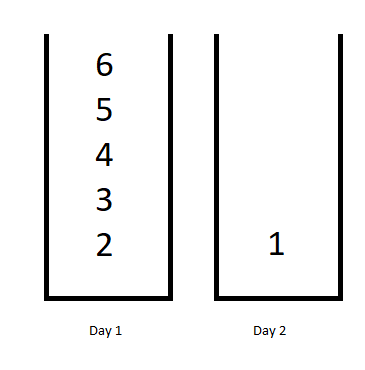
For the above example the best solution is to do the jobs with difficulty 6,5,4,3,2 in day 1 and then in day 2 just do the job number 1.
Solution
State variables and a function to solve
Let’s first find the state variables. As we solve the subproblems of the actual problem what are all the arguments that changes needs to known. If we read the problem carefully, we need to add couple of questions to solve these overlapping subproblems.
- How many jobs to add in a certain day? How it affects the future subproblem decisions? How it connects with the previous subproblem decision?
Okay, based on the first question - we could define that “day” is one of the state variables. Other state variable is “starting job number” or let’s call it index of JobDifficulty array.
Now the function that we need to solve for every subproblem is f(JobIndex, day).
For example, Initially the values passed to the function is f(1, 1). Maximum number of jobs that can be added to any particular day is equal to Total number of jobs remaining - (Total number of days remaining-current_day); Let’s call this MMM_MAX. Same formula applies to day 2, day 3, day 4……..day n, etc.
At the minimum every day at least one job needs to be allocated. Now to solve every subproblem, the function should find a value between JobIndex to MMM_MAX with the goal that at the end we find the minimal difficulty of a job schedule. (i.e) All the max elements in the array should be grouped together as much as possible in a single day.
