Dynamic programming Introduction - Part 1 👋

Quick summary ↬  Dynamic programming is a very interesting programming paradigm that could be used to explore all the possible solutions to a problem. I will provide varieties of problems that could be solved using dynamic programming paradigm.

1. When Dynamic programming

All the problems that could be solved using dynamic programming will have below characteristics:

1. The problem could be divided into “overlapping subproblems” and the solution of those overlapping subproblems could be reused multiple times.
   
2. The problem has “optimal substructure”. This means a final optimal solution could be found by finding optimal solutions to all the overlapping subproblems of the original subproblems.
   

Fibonacci series is a classic problem that can be broken down into overlapping subproblems and after finding the optimal solution to each subproblems it is used to form the optimal solution solution to the original problem.

if you wanted to find the n^th Fibonacci number F(n), you can break it into smaller subproblems such as F(n-1) and F(n-2) and find the solution to it till you reach the base case. Adding the solution together gives the solution to the original question, F(n-1) + F(n-2) = F(n). This means we can broke down the problem into overlapping subproblem and each subproblem has an optimal substructure. These subproblems are overlapping - for example to find F(7) you need to find the solution to the subproblem F(6) and F(5) and add them together.

1.1 Greedy vs Dynamic vs Divide and conquer

1. Greedy algorithms has optimal substructure, but not overlapping subproblems.
   
2. Divide and conquer can be broken down into subproblems but not overlapping.
   
3. Dynamic programming is all about overlapping subproblems and optimal substructure.

1.2 Naive idea on solving DP problems

Break the problems into smaller chunks and then find the way to SOLVE THE SMALLER SUBPROBLEMS and question yourself about how this will CONTRIBUTE to solve the larger problem at hand. Next, define the BASE CASE, define the STATE VARIABLES, TEMPORARY VARIABLES.

Dynamic programming not only helps us to solve complex problems by breaking it into subproblems but it provides us the way to improve the time and space complexity compared to brute force solutions. We can implement the dynamic programming solution using two methods which will be discussed in the next section. It is important to understand the difference so we can choose the best solution to the problem at hand.

2. Approaches to solve the Dynamic programming problem

There are two ways to implement a DP algorithm.

1. Bottom-up, well-known as Tabulation.
   
2. Top-down, well-known as Memoization.
   

2.1 Bottom-up (Tabulation)

In the bottom-up approach, we start at the BASE CASE and then we iterate using those values and solve subproblem, pass the outcome of the subproblem to solve other subproblems that depends on it. For example, if we consider the Fibonacci sequence problem, the base case is F(0)=0 and F(1)=1. With bottom-up, we would use the base case to calculate the outcome of the next subproblem. F(2) = F(0) + F(1) and we continue do this till we find the outcome of F(n).

1
2
3
4
5

F = array of length n+1 // State variables
F[0] = 0 // Base 
F[1] = 1 //Base
for i from 2 to n:   // solving the subproblems
    F[i] = F[i-1] + F[i-2]; //solving the subproblems

2.2 Top-down (Memoization)

In the Top-down approach, we start at the actual problem and not the base case. We do recursion (think about function call overhead) and the outcome of every subproblem is stored in a hash map (mostly, but feel free to think what other data structures could be used here). The idea of storing the outcome of all the subproblems in a data structure where the lookup only costs O(1) is called Memoization.

If you want to find the n^th fibnonacci number F(n), we try to compute this by finding F(n-1) and F(n-2). This defines a recursive pattern and it continues till the base case before even it computes anything useful. After reaching the base case, every recursive call returns the computed value and it is stored in the data structure defined (Memoization). Without the memoization in place there are tons of unnecessary computations.

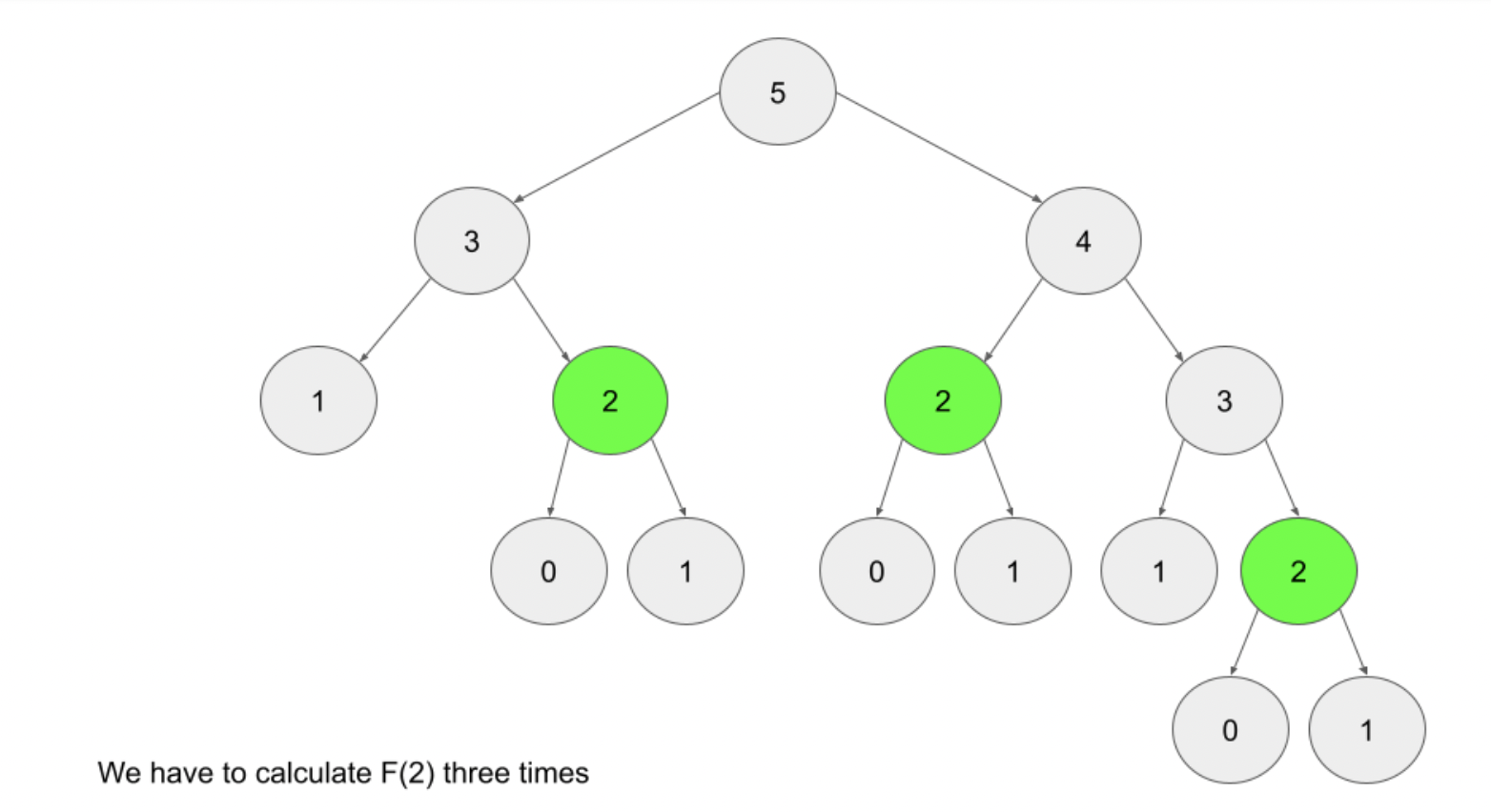
Notice the duplication on the calculation we need to do if we just do recursion without memoization which leads us to develop only a solution that runs in exponential time.

1
2
3
4
5
6
7
8

storage = hashmap
Function F(integer i) {
    if i is 0 or 1:
        return i;
    if i is not in storage:
        storage[i] = F(i-1) + F (i-2)
    return storage[i]
}

3. Conclusion

In this article, we explored dynamic programming ,two methods of it, fibonacci series, comparison with greedy, divide and conquer algos. In the next next solve couple of problems using dynamic programming and develop a framework for it.